问题背景:
数据压缩是通信和存储领域的核心技术。不管是在数据传输还是在数据存储环节,高效的缩减都可以直接提升带宽、显著降低成本。随着智能社会催生的数据量爆炸式增长,最近五至十年,全球顶尖的IT巨头们如Google和Facebook等纷纷推出各自研发的新一代压缩算法,以相比传统压缩算法更高的压缩率和更低的复杂度,实现极致压缩,从而优化通信系统的使用效率,提升用户体验。
问题定义:
数据压缩理论和Shannon在20世纪50年代建立的通信理论有密切的关系。从信息论发展的历史来看,最早的压缩理论基于对数据产生形式(“信源”)的假设。Shannon理论中的信源压缩定理建立了前缀编码的最优性理论。在信源编码定理中揭示出对随机变量X进行D进制前缀编码,其对应的最优码长满足不等式
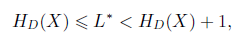
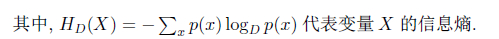
特别地,当信源序列中的字符独立同分布时,H(X)=Σt H(Xt)= TH(X1),因此可以通过对每个出现的字符进行各自编码,达到压缩的渐近最优。对于已知分布的信源,压缩率的极限直接取决于信源分布的熵。Huffman在20世纪50年代提出的编码以及80年代出现的算术编码(arithmetic coding,AC)是理论上达到最优压缩率的编码方法。实际情形中,假如信源满足分布p(X),而压缩算法通过分布q(X)来描述信源,则算法可取得的码长和(期望意义下的)最优码长间存在一个不可消除的误差,可以通过KL散度来度量:
无论怎样,对于已知或确定性概率分布的信源,无损压缩从理论和算法两个层面,都可以说已经在20世纪90年代就发展得十分成熟了。实际情形中,数据通常无法用简单的概率分布来描述或近似。对于通用场景下分布未知的信源产生的数据,Ziv和Lempel在1977至1978年设计提出了具有划时代意义的LZ77和LZ78两个算法。这两个算法的精髓在于通过滑窗和字典等技巧,将原本复杂的概率统计转化为对重复字符串的识别和替换,从而达到对几乎是任意的、分布未知的数据流的高效压缩。无损压缩与有损压缩的比较可参见图1。
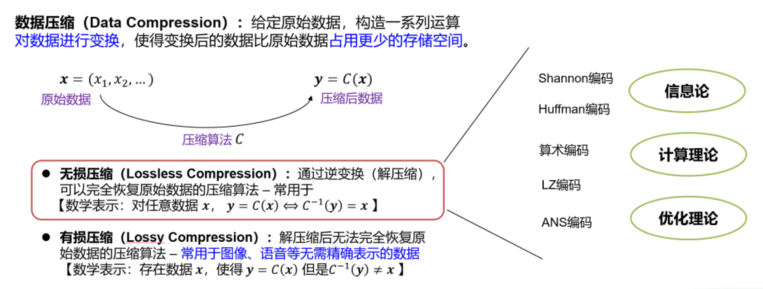
图1:无损压缩vs. 有损压缩
对于序列数据x =(xt ∈ Ω)t=1,。。。,T ,压缩可以被定义为一种函数变换(通常由对应的压缩算法来实现)C : x → y。如果变换C 是可逆的,则压缩是无损的,即,可以从压缩后的数据y 完全恢复回原始数据x;反之,假如C 不可逆,则其对应于有损压缩。
对于无损压缩,将压缩前后的数据长度分别记为L(x)= T (单位: bits)和L(y)= T′,则可以定义压缩率(有时也称为压缩比)
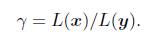
对压缩算法的研究,主要目的在于设计高效的可逆变换C,使得压缩率γ 尽可能地大。
未来研究方向:
从数据压缩的理论发展来看,无论是Huffman编码,还是LZ系列的字典编码以及算术编码等熵编码,从某种意义来说,都是“最优”压缩算法。然而,这些算法的最优性通常在数学意义上指代(数据量无限大场景下的)渐近最优,而无法对特定压缩场景下如何选择和取舍给出指导。对于给定的、有限长的数据,极致的无损压缩需要解决以下根本问题:
(1)如何(重新)定义压缩算法的最优性;
(2)如何建立基于预训练模型的压缩算法的理论框架;
(3)如何利用异构的计算环境设计高效压缩算法;
(4)如何快速识别并利用数据中重复的片段;
(5)如何在压缩率和压缩速度间达到最佳的平衡。
由于大数据时代数据呈现的复杂性、多样性和不确定性,传统的压缩算法从压缩率和数据吞吐量来看,已经无法满足对数据缩减的迫切需求。AI作为“信息自动化”的关键工具,在研究领域被广泛关注。以图像和文本为主要场景,最近五年在各个AI领域的会议和期刊上,出现了大量相关的工作,将AI强大的预测能力与传统信源编码的高效率相结合,达到压缩率与压缩速度的平衡。从未来研究角度,尚有许多值得探索的方向:
(1)基于AI的通用数据压缩方法;
(2)数据的多尺度和相似重删;
(3)数据库等结构类数据的高效压缩。
将AI理论和前沿技术引入数据压缩领域的尝试还处于较为初级的发展阶段。从已有的研究来看,由于算法复杂度过高,现有AI压缩方法在带来压缩率提升的同时,其处理数据的速度离实际需求的差距巨大。特别地,对于通用场景,暂时还并未有确切的研究结论支持AI压缩相较于传统方法的优越性。从另一个角度而言,正如深度学习本身在各个领域的成功通常对应着特定的模型和算法设计,基于AI的压缩方法极有可能沿着类似的方式发展。即,针对不同类型的数据,基于对应的领域知识中发展得到的AI工具将有潜力催生第一批实用的新一代压缩算法。例如:
(1)文本数据:NLP等上下文模型;
(2)声音等物理信号:时域频域的对应模型和时间序列预测;
(3)网页数据:混合数据的识别、重删和重组;
(4)数据库数据:结构化数据的智能识别和关联预测;
(5)图像和视频:多维度以及多尺度预测。
其中,声音、图像和视频等信号数据基于模拟信号的采样而得,通常不需要精确无损的压缩编码,因此在AI模型的选择和设计上,或许有更灵活的探索方式和研究空间。此处主要探讨的是对于原始信号的无损恢复。


