问题背景:
近三十年来,现代编码采取概率译码取得性能的大幅突破。随着 Turbo码、LDPC码与 Polar码等编码的演进,长码逐渐逼近了信道容量极限。即便如此,多数应用仍使用经典代数编码而非现代编码,其主要原因为:
(1)现代编码多使用迭代译码,功耗与时延都比经典代数译码多上几个数量级;
(2)概率译码需要软信息,许多应用无法获取软信息;单纯比较硬判决性能,经典代数编码在中短码长下优于现代编码;
(3)现代编码即便使用软判决,其中短码的性能仍不及经典代数编码(如图1)。
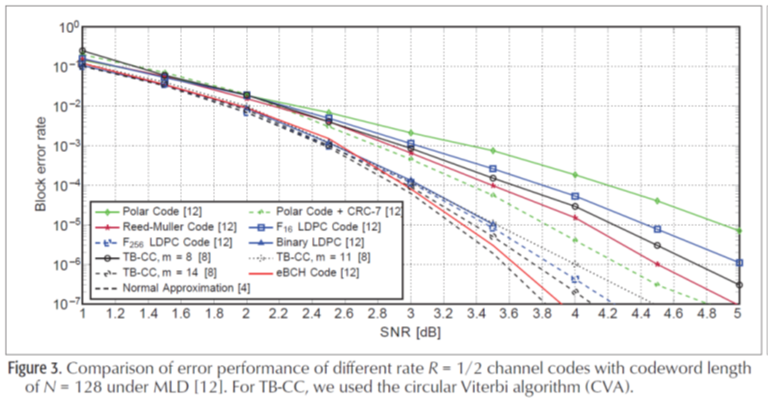
图1:码长128 比特的编码方案比较跟现代编码比较,BCH代数编码拥有更优的性能
经典代数编码中,最广为使用的是Reed-Solomon码。Reed-Solomon码在 1960年被 Irving S。Reed 和 Gustave Solomon发明后,因为其优美的代数结构被应用在通信和存储领域,如存储介质的CD与 DVD、存储系统的纠删编码、通信系统的光通信与无线通信、密码、甚至是我们日常使用的二维码。随着未来半导体工艺往更高的集成度、低电压和高开关速度发展,半导体内部的电子迁移、材料的相变和电子自旋特性等都出现大量的概率性质,而计算和存储的速度一般在纳秒和微秒尺度,经典的迭代和软译码不适宜此类场景,需要探索更加高效的代数编码。
然而,Reed-Solomon 码构造在二变量多项式(bivariate polynomial)上可看作有限域上的直线,其码长受限于所操作的有限域大小而无法突破 Gilbert-Varshamov 界。如在有限域大小为 64情况下,Reed-Solomon码长最多为 63;而作为代数几何码,Hermite码的码长却可达512。也因为码长的限制,Reed-Solomon 码在有些应用上被现代编码所取代(如 FLASH 存储的纠错编码)。如果代数几何码的编译码速度能提升至与 Reed-Solomon 编译码相同的量级,将可以取代现今仍广泛应用的 Reed-Solomon 编码并提供更低功耗、更低时延的编码方案,带来重大变革。
问题定义:
代数几何码的编译码问题本身是非常困难的。自 Goppa于1970年代提出代数几何码以来,Garcia 和Stichtenoth在1995年左右提出的通用编码算法,在2001年才被Shum等改善,但改善后其复杂度仍有O(n3);而在译码方面,Feng和 Rao在1993年利用多数投票(majority voting)原则设计出通用的译码算法,但复杂度也为 O(n3)。代数几何码的通用快速编译码算法长期以来都是学术界与工业界关注的重要难题。相较于 Reed-Solomon 编译码的发展,代数几何码目前只有小幅进展,离广泛投入实际应用还有很大差距。目前关于代数几何码的主要研究问题有:
(1) 构造具有良好参数的代数几何码(“好码”),使得其信息率和相对最小 Hamming 距离在渐近意义下超过一些经典的下界(如Gilbert-Varshamov下界、以及后续改进的Tsfasman-Vladut-Zink下界等)。
(2) 设计代数几何码的快速编译码算法,如:复杂度低于 O(n2)的通用代数几何编译码算法,或针对特殊代数几何码更快速的编译码算法。由于现实应用对编码与译码速度的需求,快速编译码问题目前是代数几何码纳入实际应用的主要瓶颈。
(3) 推广高度发展的Reed-Solomon编译码算法到代数几何码,有效降低现有算法复杂度。
未来研究方向:
关于代数几何码的快速译码问题,有如下几个需要进一步研究的问题:
(1) 针对代数几何码开发快速的通用编译码算法,目标是降低编码与译码算法复杂度到 O(n2)以下;
(2) 设计特殊代数曲线,使编码效能可达Tsfasman-Vladut-Zink下界并且存在快速编译码算法;
(3) 受现有Reed-Solomon 编译码算法启发,特别是快速傅里叶变换算法,使其可以套用在代数几何码,目标是针对特定代数曲线可达到编码复杂度 O(n log r)且纠错复杂度 O(n log r + r log logr)。


